Ученые СПбПУ внесли значительный вклад в изучение природы квазикристаллов
Драгоценные камни, металлические сплавы – кристаллы вокруг нас. Они прекрасны, интересны и порой непонятны. Проблемами кристаллографии занимаются многие ученые. Особенный интерес представляют удивительные «как будто кристаллы» – квазикристаллы. Их тернистый путь в науке стоил огромных усилий ученым, которые занимались их изучением, и до сих пор многие их тайны не разгаданы. Однако можно не сомневаться, что с точки зрения практического материаловедения эти усилия в будущем окупятся сторицей.
Они обладают высокой трещиностойкостью и стойкостью к истиранию. Сплавы легких элементов, имеющие квазикристаллическую структуру, используются для создания материалов с заранее заданными свойствами для авиационной и аэрокосмической промышленности. Они также используются для получения сверхпрочных сталей, например для изготовления медицинских игл. Фотонные квазикристаллы могут быть перспективны для активных элементов в волоконно-оптических линиях связи. Кроме того, сейчас разработана технология нанесения квазикристаллических покрытий для создания термических барьеров (например, покрытие на сковородке, в качестве рабочей поверхности для приготовления пищи).
В 1982 году Дан Шехтман, ученый из Техниона – Израильского технологического института города Хайфа, проходя стажировку в Национальном институте стандартов и технологий (США), изучал быстроохлажденные сплавы алюминия с переходными металлами при помощи дифракции электронов и впервые наблюдал симметрию пятого порядка на дифракционных картинах. Согласно основной теореме кристаллографии, такого быть не могло в принципе. Позже такие материалы были названы квазикристаллами. Долгий путь, начавшийся с полного неприятия многими коллегами обнаруженного факта, привел в итоге к присуждению в 2011 году Дану Шехтману Нобелевской премии за открытие, в экстремальной степени противоречившее доминировавшей на тот момент теории. Международный союз кристаллографов вынужден был признать устаревшим прежнее определение кристаллов. Самое короткое и в то же время математически строгое определение дал Фримен Дайсон: «Кристалл – это чисто точечное распределение с чисто точечным спектром». Это определение включает в себя в качестве специального случая и обычные кристаллы как периодические распределения с периодическими спектрами.
В 1984 году Пол Стейнхардт, ныне директор Центра теоретической науки в Принстоне, смог дать первое теоретическое объяснение структуры икосаэдрических квазикристаллов при помощи проецирования шестимерной периодической решетки в трехмерное пространство, ориентированное под иррациональным углом. Процедура проецирования очень сложна и не всегда однозначна. Поэтому вопрос, где же расположены атомы в структурах реальных квазикристаллов, по-прежнему остается актуальным.
Санкт-Петербургский политехнический университет не остался в стороне от изучения столь интересного и перспективного направления в материаловедении. До настоящего времени считалось, что описание структуры икосаэдрических квазикристаллов иначе как при помощи шестимерного пространства невозможно. Ведущим научным сотрудником Центра перспективных исследований СПбПУ Алексеем Евгеньевичем Мадисоном был опубликован ряд статей, внесших существенный теоретический вклад в изучение их структуры и в понимание природы квазикристаллов в целом. Основные статьи были опубликованы в журнале «RSC Advances» Королевского химического общества, а иллюстрация из другой его статьи украсила обложку одного из выпусков иностранного журнала «Structural Chemistry» издательства «Springer».

Основываясь на выведенных им правилах подстановок, Алексею Евгеньевичу удалось сформулировать строгий рекурсивный итерационный алгоритм, позволяющий заполнить все пространство четырьмя типами так называемых «золотых» зоноэдров. Зоноэдры четырех типов – ромбический триаконтаэдр (тридцатигранник) Кеплера, двадцатигранник Федорова, двенадцатигранник Билинского и вытянутый ромбоэдр – увеличиваются в иррациональном масштабе, равном кубу золотого сечения, и затем вновь заполняются копиями исходных многогранников. По сути, есть 4 типа многогранников, каждый из них увеличивается и заполняется исходными копиями всех 4-х типов вышеперечисленных многогранников. Но каждый раз увеличенная копия снова содержит все 4 типа многогранников, каждый из которых после увеличения снова содержит копии всех 4-х и, в том числе, копии самого себя. Получается запутанный алгоритм, когда при заполнении всех 4-х увеличенных многогранников на каждом следующем этапе нужно знать, как все 4 уже заполнены на предыдущем шаге.
В результате в работе А.Е. Мадисона были выведены все три неэквивалентные упаковки атомов с точной икосаэдрической симметрией, на существование которых указывал Пол Стейнхардт. Были сформулированы «естественные» правила локального соответствия, согласно которым существует 2 типа неэквивалентых узлов, 2 типа ребер, 3 типа граней и 4 типа квази-ячеек. Самый важный достигнутый результат его работы – это то, что для описания структуры икосаэдрических упаковок атомов больше нет необходимости в привлечении шестимерного пространства. По крайней мере, теперь появилась реальная альтернатива многомерному подходу.
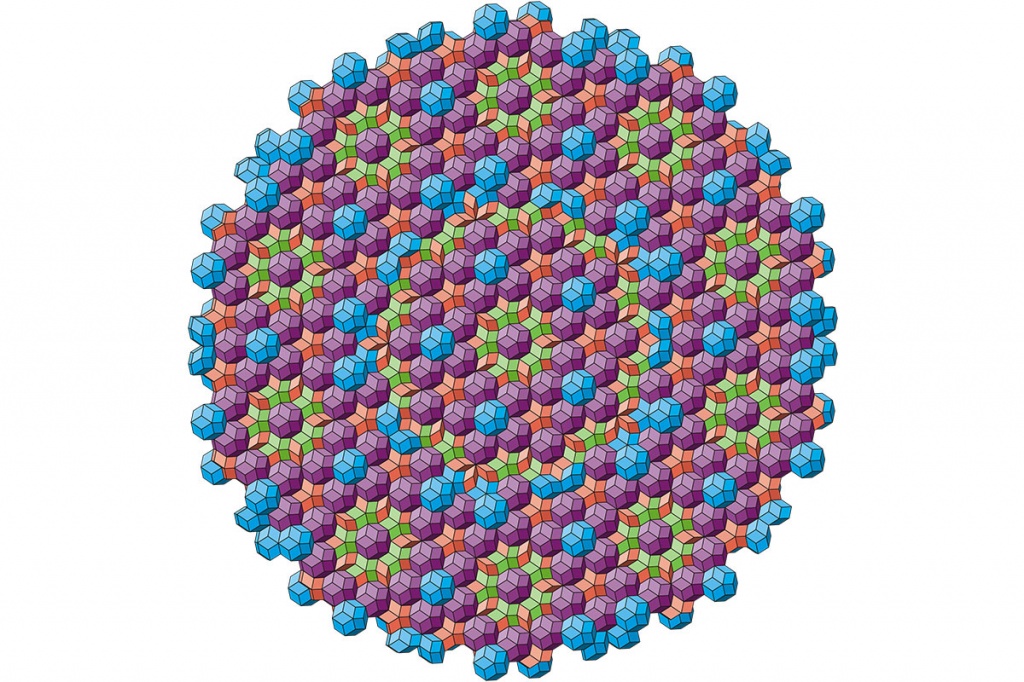
В качестве примера на рисунке приведена одна из трех возможных идеальных икосаэдрических структур в проекции вдоль оси пятого порядка. Четыре типа квазиэлементарных ячеек обозначены четырьмя различными цветами.
Алексей Евгеньевич сообщил, что недавно с помощью разработанного им метода удалось описать одну из важнейших реальных квазикристаллических структур (статья готовится к публикации).
Материал подготовлен Медиа-центром СПбПУ
